The importance of interactive control variables when testing interactive hypotheses

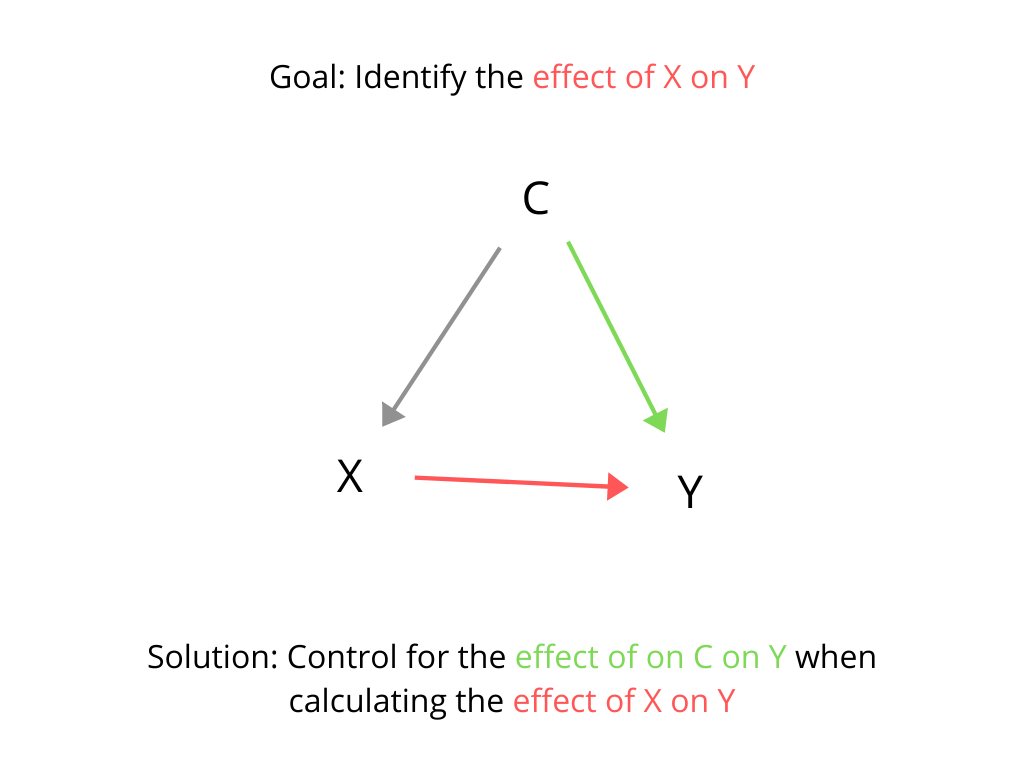
Including control variables in a regression model is common practice in many fields of scientific research. This is often done because the researcher is concerned that some third variable may be a confounding variable when attempting to identify the effect of the primary predictor variable of interest on the outcome of interest. For example, if a researcher's primary goal is to identify the effect of X on Y, but there is some other variable C that affects both X and Y, then it will be difficult to identify the effect of X on Y because the effects of C would generate correlation between X and Y even in the absence of any causal relationship between X and Y. Conditioning on C when calculating the correlation between X and Y can allow a researcher to control for that confounding effect. This is can be done by measuring C and including its effect on Y in the model when modeling the effect of X on Y. (For a more detailed explanation of the concept of control variables, see http://jamescragun.com/teaching/what_does_controlling_for_mean.html)

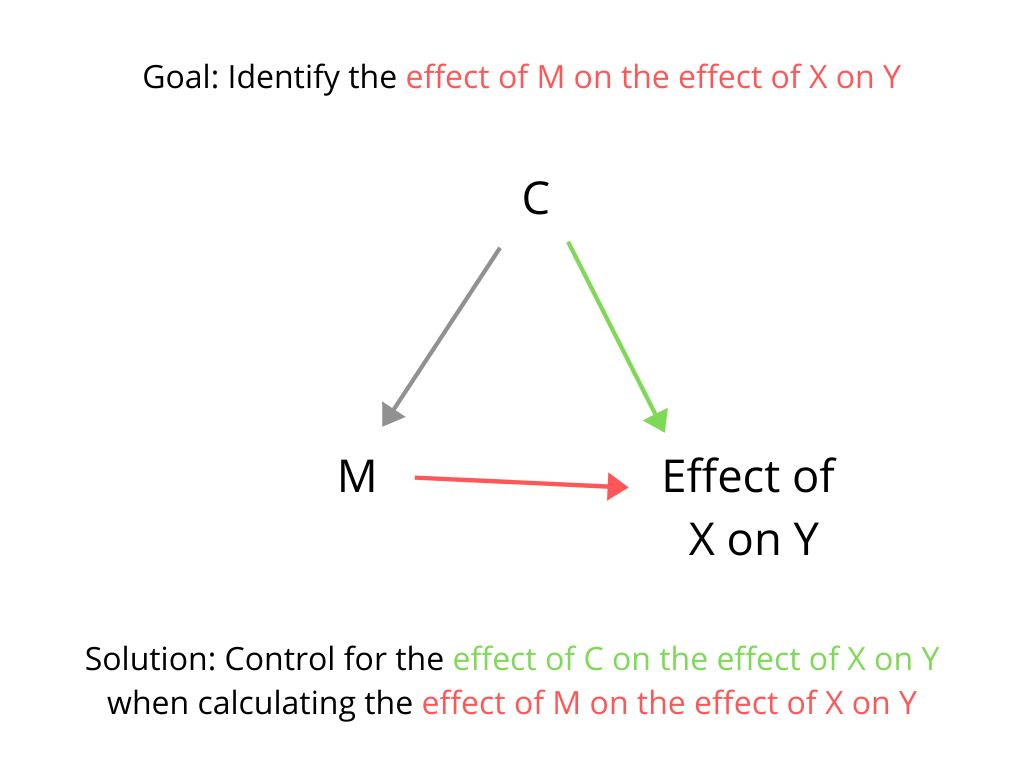
However, suppose the researcher's primary goal is not just to test whether the value of Y depends on X, but rather to test whether the effect of X on Y depends on the value of M, a hypothesized moderating variable. In other words, the researcher wants to identify the effect of M on the effect of X on Y. This is often done using a multiplicative interaction between M and X in a model of Y. However, it is important to remember that although the outcome variable in the model is Y, the outcome of primary interest is the effect of X on Y. The researcher is not just trying to identify the effect of M on Y but rather trying to identify the effect of M on the effect of X on Y. If some other confounding variable C affects the effect of X on Y, and if C also affects M, then it will be difficult to identify the effect of M on the effect of X on Y because C will generate correlation between M and the effect of X on Y even in the absence of any direct causal relationship between M and the effect of X on Y. This problem can be alleviated by controlling for the effect of C on the effect of X on Y when calculating the correlation between M and the effect of X on Y. In a model of Y (that includes an interaction between M and X in an attempt to idenitify the effect of M on the effect of X on Y), we can control for the effect of C on the effect of X on Y by including an interaction between C and X in the model. Simply adding C to the model of Y will not control for this confound. Including C in the model controls for simple additive effects of C on Y but does not control for the effect of C on the effect of X on Y. To control for the effect of C on the effect of X on Y, the model would need to include an interaction between C and X.

Example

A hypothetical example may help make these concepts more clear. Suppose you theorize that people who support tax cuts feel more positively about the current president. Suppose further that you are not only interested in testing whether this effect of tax-cut attitudes on support for the president exists. Rather, you are interested in testing whether this effect depends on a person’s income. You theorize that having more income causes a stronger correlation between a person’s support for tax cuts and the person’s level of support for the president.

One way you might try to test this is by estimating a model of support for the president, while including the following variables in the model: income, support for tax cuts, and a multiplicative interaction between the two. A positive coefficient on the interactive term would indicate that the correlation between support for tax cuts and support for the president is greater (more positive or less negative) among people who have higher income.

However, this doesn’t necessarily suggest that higher income causes this greater correlation. There could be some confounding variable. Suppose you suspect that a person’s education level might be a confound because income is affected by education, and you are concerned that the effect might actually be driven by education rather than by income. Perhaps having more education could make a person more likely to recognize whether the president’s policies align with their own policy preferences. Or perhaps there is some other demographic variable (other than income or education) that is responsible for the effect.

To test whether the estimated effect of income remains even when conditioning on education and on several other demographic variables, you try adding education and the other demographic variables to the model as control variables. The model now includes income, education, support for tax cuts, several other variables, and a multiplicative interaction between income and support for tax cuts. Suppose you find that the coefficient on the interactive term is still positive, even when including all these control variables in the model. If you were to conclude from this that you now have stronger evidence that income directly affects the strength of the association between support for tax cuts and support for the president, you would be wrong.

The problem here is that education may affect the relationship between support for tax cuts and support for the president. This, combined with education’s possible effect on income, is what makes education a potential confounding variable. You did not eliminate this problem because you did not actually control for the effect of education on the relationship between support for tax cuts and support for the president. You simply controlled for the effect of education on support for the president. To control for the effect of education on the relationship between support for tax cuts and support for the president, you would need a model that estimates the effect of education on the relationship between support for tax cuts and support for the president. In other words, if support for the president is the model’s outcome variable, the model would need to include a multiplicative interaction between education and support for tax cuts. If you also wish to add other potential confounding variables to the model as control variables, you also need to include an interaction between support for tax cuts and each control variable.

Estimation bias

Let's put this in more precise mathematical terms. Suppose the true data-generating process is:

Y_i = βX_i + δM_i + γX_iM_i + ζC_i + ηC_iX_i + ε_i

However, suppose you try to estimate a model that excludes the C_iX_i interactive term:

Y_i = α' + β'X_i + δ'M_i + γ'X_iM_i + ζ'C_i + ε_i

In this mis-specified model, the expected value of the estimated interaction coefficient γ' is:

E(γ') = γ + η ( ^{cov(C, M)} / _var(M) )

If the covariance of C and M is zero, or if η (the interactive effect of C_iX_i on Y) is zero, then the expected value of the estimated interaction coefficient γ' is equal to the true value of the interaction coefficient γ. If not, the estimate is biased.

Estimation bias demonstrated in simulations

I have created simulations to demonstrate in what situations the failure to include an interactive control variable is most problematic. Here I have created an easy-to-use interactive web version of some of my simulations:

https://jamescragun.shinyapps.io/the_importance_of_interactive_control_variables/

In this interactive simulation, you can adjust the parameters of the true model to see which situations result in large biases when attempting to estimate the interaction effect. Depending on the parameters you choose, the code will produce plots that look something like this:

My current research

Unfortunately, many scientists, when testing interactive hypotheses, believe they can control for confounds by including only additive control variables in their models. I am currently reviewing the political science literature to determine how common this type of mistake is in published research.